Subsections of Tries
Introduction to Tries
Introduction to Tries
A trie is a nonempty tree storing a set of words in the following way:
- Each child of a node is labeled with a character.
- Each node contains a boolean indicating whether the labels in the
path from the root to that node form a word in the set.
The word, “trie”, is taken from the middle of the word, “retrieval”, but
to avoid confusion, it is pronounced like “try” instead of like “tree”.
Suppose, for example, that we want to store the following words:
- ape
- apple
- cable
- car
- cart
- cat
- cattle
- curl
- far
- farm
A trie storing these words (where we denote a value of true for the
boolean with a *) is as follows:
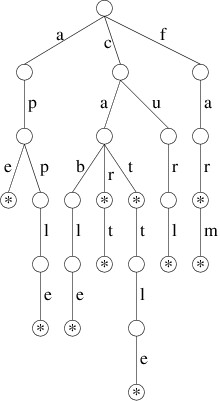

Thus, for example, if we follow the path from the root through the
labels ‘c’, ‘a’, and ‘r’, we reach a node with a true boolean value
(shown by the * in the above picture); hence, “car” is in this set of
words. However, if we follow the path through the labels ‘c’, ‘u’, and
‘r’, the node we reach has a false boolean; hence, “cur” is not in
this set. Likewise, if we follow the path through ‘a’, we reach a node
from which there is no child labeled ‘c’; hence, “ace” is not in this
set.
Note that each subtree of a trie is also a trie, although the “words” it
stores may begin to look a little strange. For example if we follow the
path through ‘c’ and ‘a’ in the above figure, we reach a trie that
contains the following “words”:
- “ble”
- “r”
- “rt”
- “t”
- “ttle”
These are actually the completions of the original words that begin
with the prefix “ca”. Note that if, in this subtree, we take the path
through ’t’, we reach a trie containing the following completions:
- "" [i.e., the empty string]
- “tle”
In particular, the empty string is a word in this trie. This motivates
an alternative definition of the boolean stored in each node: it
indicates whether the empty string is stored in the trie rooted at this
node. This definition may be somewhat preferable to the one given above,
as it does not depend on any context, but instead focuses entirely on
the trie rooted at that particular node.
One of the main advantages of a trie over an AVL
tree
is the speed with
which we can look up words. Assuming we can quickly find the child with
a given label, the time we need to look up a word is proportional to the
length of the word, no matter how many words are in the trie. Note that
in looking up a word that is present in an AVL tree, we will at least
need to compare the given word with its occurrence in the tree, in
addition to any other comparisons done during the search. The time it
takes to do this one comparison is proportional to the length of the
word, as we need to verify each character (we actually ignored the cost
of such comparisons when we analyzed the performance of AVL trees).
Consequently, we can expect a significant performance improvement by
using a trie if our set of words is large.
Let’s now consider how we can implement a trie. There are various ways
that this can be done, but we’ll consider a fairly straightforward
approach in this section (we’ll improve the implementation in the next
section
). We
will assume that the words we are storing are comprised of only the 26
lower-case English letters. In this implementation, a single node will
contain the following private fields:
- A bool storing whether the empty string is contained in the trie
rooted at this node (or equivalently, whether this node ends a word
in the entire trie).
- A 26-element array of nullable tries storing the children, where element 0
stores the child labeled ‘a’, element 1 stores the child labeled
‘b’, etc. If there is no child with some label, the corresponding
array element is null.
For maintainability, we should use private constants to store the above array’s size (i.e., 26) and the first letter of the alphabet (i.e., ‘a’). Note that in this implementation, other than this last constant, no chars or strings are
actually stored. We can see if a node has a child labeled by a given
char by finding the difference between that char and and the first letter of the alphabet, and
using that difference as the array index. For example, suppose the array
field is named _children, the constant giving the first letter of the alphabet is _alphabetStart, and label is a char variable
containing a lower-case letter. Because char is technically a
numeric type, we can perform arithmetic with chars; thus, we can
obtain the child labeled by label by retrieving
_children[label - _alphabetStart]. More specifically, if _alphabetStart is ‘a’ and label
contains ’d’, then the difference, label - _alphabetStart, will be 3; hence,
the child with label ’d’ will be stored at index 3. We have therefore
achieved our goal of providing quick access to a child with a given
label.
Let’s now consider how to implement a lookup. We can define a public
method for this purpose within the class implementing a trie node:
public bool Contains(string s)
{
. . .
}
Note
This method does not need a trie node as a parameter because
the method will belong to a trie node. Thus, the method will be able to
access the node as
this
, and may
access its private fields directly by their names.
The method
consists of five cases:
s is null. Note that even though s is not defined to be nullable, because the method is public, user code could still pass a null value. In this case, we should throw an ArgumentNullException, provides more information than does a NullReferenceException.s is the empty string. In this case the bool stored in
this node indicates whether it is a word in this trie; hence, we can
simply return this bool.- The first character of
s is not a lower-case English letter (i.e.,
it is less than ‘a’ or greater than ‘z’). The constants defined for this class should be used in making this determination. In this case, s can’t be stored
in this trie; hence, we can return false.
- The child labeled with the first character of
s (obtained as
described above) is missing (i.e., is null). Then s isn’t
stored in this trie. Again, we return false.
- The child labeled with the first character of
s is present (i.e.,
non-null). In this case, we need to determine whether the
substring following the first character of s is in the trie rooted
at the child we retrieved. This can be found using a recursive call
to this method within the child trie node. We return the result of
this recursive call.
In order to be able to look up words, we need to be able to build a trie
to look in. We therefore need to be able to add words to a trie. It’s
not practical to make a trie node immutable, as there is too much
information that would need to be copied if we need to replace a node
with a new one (we would need to construct a new node for each letter of
each word we added). We therefore should provide a public method
within the trie node class for the purpose of adding a word to the trie
rooted at this node:
public void Add(string s)
{
. . .
}
This time there are four cases:
s is null. This case should be handled as in the Contains method above.s is the empty string. Then we can record this word by setting
the bool in this node to true.- The first character of
s is not a lower-case English letter. Then
we can’t add the word. In this case, we’ll need to throw an
exception.
- The first character is a lower-case English letter. In this case, we
need to add the substring following the first character of
s to
the child labeled with the first letter. We do this as follows:
- We first need to make sure that the child labeled with the first letter of
s is non-null. Thus, if this child is null, we construct a new trie node and place
it in the array location for this child.
- We can now
add the substring following the first letter of
s to this child by
making a recursive call.
Multiple Implementations of Children
Multiple Implementations of Children
The trie implementation given in the previous
section
offers very
efficient lookups - a word of length
$ m $ can be looked up in
$ O(m) $
time, no matter how many words are in the trie. However, it wastes a
large amount of space. In a typical trie, a majority of the nodes will
have no more than one child; however, each node contains a 26-element
array to store its children. Furthermore, each of these arrays is
automatically initialized so that all its elements are null. This
initialization takes time. Hence, building a trie may be rather
inefficient as well.
We can implement a trie more efficiently if we can customize the
implementation of a node based on the number of children it has. Because
most of the nodes in a trie can be expected to have either no children
or only one child, we can define alternate implementations for these
special cases:
- For a node with no children, there is no need to represent any
children - we only need the bool indicating whether the trie
rooted at this node contains the empty string.
- For a node with exactly one child, we maintain a single reference to
that one child. If we do this, however, we won’t be able to infer
the child’s label from where we store the child; hence, we also need
to have a char giving the child’s label. We also need the
bool indicating whether the trie rooted at this node contains
the empty string.
For all other nodes, we can use an implementation similar to the one
outlined in the previous
section
. We will still
waste some space with the nodes having more than one child but fewer
than 26; however, the amount of space wasted will now be much less.
Furthermore, in each of these three implementations, we can quickly
access the child with a given label (or determine that there is no such
child).
Conceptually, this sounds great, but we run into some obstacles as soon
as we try to implement this approach. Because we are implementing nodes
in three different ways, we need to define three different classes. Each
of these classes defines a different type. So how do we build a trie
from three different types of nodes? In particular, how do we define the
type of a child when that child may be any of three different types?
The answer is to use a C# construct called an interface. An interface
facilitates abstraction - hiding lower-level details in order to focus
on higher-level details. At a high level (i.e., ignoring the specific
implementations), these three different classes appear to be the same:
they are all used to implement tries of words made up of lower-case
English letters. More specifically, we want to be able to add a
string to any of these classes, as well as to determine whether they
contain a given string. An interface allows us to define a type that
has this functionality, and to define various sub-types that have
different implementations, but still have this functionality.
A simple example of an interface is
IComparable<T>
.
Recall from the section, “Implementing a Dictionary with a Linked
List”
,
that we can constrain the keys in a dictionary implementation to be of a
type that can be ordered by using a where clause on the class
statement, as follows:
public class Dictionary<TKey, TValue> where TKey : notnull, IComparable<TKey>
The source code for the IComparable<T>
interface
has been posted by Microsoft®. The essential part of this definition
is:
public interface IComparable<in T>
{
int CompareTo(T? other);
}
(Don’t worry about the in keyword with the type parameter in the
first line.) This definition defines the type IComparable<T> as
having a method CompareTo that takes a parameter of the generic type
T? and returns an int. Note that there is no public or
private access modifier on the method definition. This is because
access modifiers are disallowed within interfaces — all definitions are
implicitly public. Note also that there is no actual definition of
the CompareTo method, but only a header followed by a semicolon.
Definitions of method bodies are also disallowed within interfaces — an
interface doesn’t define the behavior of a method, but only how it
should be used (i.e., its parameter list and return type). For this
reason, it is impossible to construct an instance of an interface
directly. Instead, one or more sub-types of the interface must be
defined, and these sub-types must provide definitions for the behavior
of CompareTo. As a result, because the Dictionary<TKey,
TValue> class restricts type TKey to be a sub-type of
IComparable<T>, its can use the CompareTo method of any
instance of type TKey.
Now suppose that we want to define a class Fraction and use it as a
key in our dictionary implementation. We would begin the class
definition within Visual Studio® as follows:
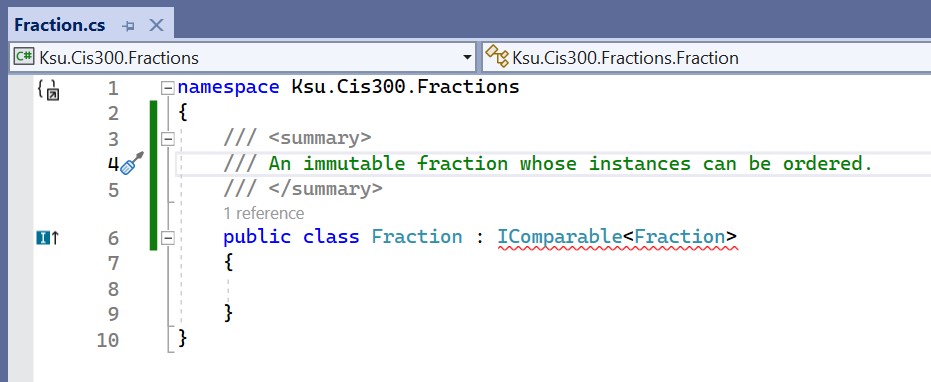
At the end of the first line of the class definition, : IComparable<Fraction> indicates that the class being defined is a
subtype of IComparable<Fraction>. In general, we can list one or
more interface names after the colon, separating these names with
commas. Each name that we list requires that all of the methods,
properties, and indexers
from that interface must be fully defined within this class. If we hover
the mouse over the word, IComparable<Fraction>, a drop-down menu
appears. By selecting “Implement interface” from this menu, all of the
required members of the interface are provided for us:
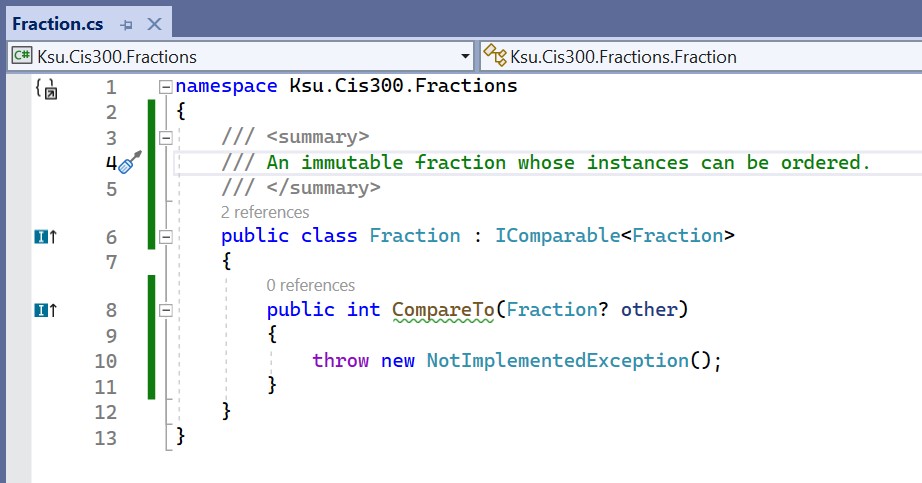
Note
In order to implement a method specified in an interface, we
must define it as public.
We now just need to replace the throw
with the proper code for the CompareTo method and fill in any other
class members that we need; for example:
namespace Ksu.Cis300.Fractions
{
/// <summary>
/// An immutable fraction whose instances can be ordered.
/// </summary>
public class Fraction : IComparable<Fraction>
{
/// <summary>
/// Gets the numerator.
/// </summary>
public int Numerator { get; }
/// <summary>
/// Gets the denominator.
/// </summary>
public int Denominator { get; }
/// <summary>
/// Constructs a new fraction with the given numerator and denominator.
/// </summary>
/// <param name="numerator">The numerator.</param>
/// <param name="denominator">The denominator.</param>
public Fraction(int numerator, int denominator)
{
if (denominator <= 0)
{
throw new ArgumentException();
}
Numerator = numerator;
Denominator = denominator;
}
/// <summary>
/// Compares this fraction with the given fraction.
/// </summary>
/// <param name="other">The fraction to compare to.</param>
/// <returns>A negative value if this fraction is less
/// than other, 0 if they are equal, or a positive value if this
/// fraction is greater than other or if other is null.</returns>
public int CompareTo(Fraction? other)
{
if (other == null)
{
return 1;
}
long prod1 = (long)Numerator * other.Denominator;
long prod2 = (long)other.Numerator * Denominator;
return prod1.CompareTo(prod2);
}
// Other class members
}
}
Note
The CompareTo method above is not recursive. The
CompareTo method that it calls is a member of the long
structure, not the Fraction class.
As we suggested above, interfaces can also include properties. For
example,
ICollection<T>
is a generic interface implemented by both arrays and the class
List<T>
.
This interface contains the following member (among others):
This member specifies that every subclass must contain a property called
Count with a getter. At first, it would appear that an array does
not have such a property, as we cannot write something like:
int[] a = new int[10];
int k = a.Count; // This gives a syntax error.
In fact, an array does contain a
Count property, but this property is available only when the array
is treated as an ICollection<T> (or an
IList<T>
,
which is an interface that is a subtype of ICollection<T>, and is
also implemented by arrays). For example, we can write:
int[] a = new int[10];
ICollection<int> col = a;
int k = col.Count;
or
int[] a = new int[10];
int k = ((ICollection<int>)a).Count;
This behavior occurs because an array explicitly implements the
Count property. We can do this as follows:
public class ExplicitImplementationExample<T> : ICollection<T>
{
int ICollection<T>.Count
{
get
{
// Code to return the proper value
}
}
// Other class members
}
Thus, if we create an instance of
ExplicitImplementationExample<T>, we cannot access its Count
property unless we either store it in a variable of type
ICollection<T> or cast it to this type. Note that whereas the
public access modifier is required when implementing an interface
member, neither the public nor the private access modifier is
allowed when explicitly implementing an interface member.
We can also include
indexers
within
interfaces. For example, the IList<T> interface is defined as
follows:
public interface IList<T> : ICollection<T>
{
T this[int index] { get; set; }
int IndexOf(T item);
void Insert(int index, T item);
void RemoveAt(int index);
}
The : ICollection<T> at the end of the first line specifies that
IList<T> is a subtype of ICollection<T>; thus, the interface
includes all members of ICollection<T>, plus the ones listed. The
first member listed above specifies an indexer with a get accessor and a
set accessor.
Now that we have seen a little of what interfaces are all about, let’s
see how we can use them to provide three different implementations of
trie nodes. We first need to define an interface, which we will call
ITrie, specifying the two public members of our previous
implementation of a trie
node
. We do, however,
need to make one change to the way the Add method is called. This
change is needed because when we add a string to a trie, we may need
to change the implementation of the root node. We can’t simply change
the type of an object - instead, we’ll need to construct a new instance
of the appropriate implementation. Hence, the Add method will need
to return the root of the resulting trie. Because this node may have any
of the three implementations, the return type of this method should be
ITrie. Also, because we will need the constants from our previous implementation in each of the implementations of ITrie, the code will be more maintainable if we include them once within this interface definition. Note that this will have the effect of making them public. The ITrie interface is therefore as follows:
/// <summary>
/// An interface for a trie.
/// </summary>
public interface ITrie
{
/// <summary>
/// The first character of the alphabet we use.
/// </summary>
const char AlphabetStart = 'a';
/// <summary>
/// The number of characters in the alphabet.
/// </summary>
const int AlphabetSize = 26;
/// <summary>
/// Determines whether this trie contains the given string.
/// </summary>
/// <param name="s">The string to look for.</param>
/// <returns>Whether this trie contains s.</returns>
bool Contains(string s);
/// <summary>
/// Adds the given string to this trie.
/// </summary>
/// <param name="s">The string to add.</param>
/// <returns>The resulting trie.</returns>
ITrie Add(string s);
}
We will then need to define three classes, each of which implements the
above interface. We will use the following names for these classes:
- TrieWithNoChildren will be used for nodes with no children.
- TrieWithOneChild will be used for nodes with exactly one child.
- TrieWithManyChildren will be used for all other nodes; this will
be the class described in the previous
section
with a few
modifications.
These three classes will be similar because they each will implement the
ITrie interface. This implies that they will each need a
Contains method and an Add method as specified by the interface
definition. However, the code for each of these methods will be
different, as will other aspects of the implementations.
Let’s first discuss how the TrieWithManyChildren class will differ from the class described in the previous
section
. First, its class statement will need to be modified to make the class implement the ITrie interface. This change will introduce a syntax error because the Add method in the ITrie interface has a return type of ITrie, rather than void. The return type of this method in the TrieWithManyChildren class will therefore need to be changed, and at the end this will need to be returned. Because the constants have been moved to the ITrie interface, their definitions will need to be removed from this class definition, and each occurrence will need to be prefixed by “ITrie.”. Throughout the class definition, the type of any trie should be made ITrie, except where a new trie is constructed in the Add method. Here, a new TrieWithNoChildren should be constructed.
Finally, a constructor needs to be defined for the TrieWithManyChildren class. This constructor will be used by the TrieWithOneChild class when it needs to add a new child. Because a TrieWithOneChild cannot have two children, a TrieWithManyChildren will need to be constructed instead. This constructor will need the following parameters:
- A string giving the string that the TrieWithOneChild class needs to add.
- A bool indicating whether the constructed node should contain the empty string.
- A char giving the label of the child stored by the TrieWithOneChild.
- An ITrie giving the one child of the TrieWithOneChild.
After doing some error checking to make sure the given string and ITrie are not null and that the given char is in the proper range, it will need to store the given bool in its bool field and store the given ITrie at the proper location of its array of children. Then, using its own Add method, it can add the given string.
Let’s now consider the TrieWithOneChild class. It will need three private fields:
- A bool indicating whether this node contains the empty string.
- A char giving the label of the only child.
- An ITrie giving the only child.
As with the TrieWithManyChildren class the TrieWithOneChild class needs a constructor to allow the TrieWithNoChildren class to be able to add a nonempty string. This constructor’s parameters will be a
string to be stored (i.e., the one being added) and a bool
indicating whether the empty string is also to be stored.
Furthermore, because the empty string can always be added to a
TrieWithNoChildren without constructing a new node, this constructor
should never be passed the empty string. The constructor can then
operate as follows:
- If the given string is null, throw an ArgumentNullException.
- If the given string is empty or begins with a character that is
not a lower-case English letter, throw an exception.
- Initialize the bool field with the given bool.
- Initialize the char field with the first character of the given
string.
- Initialize the ITrie field with the result of constructing a new
TrieWithNoChildren and adding to it the substring of the given
string following the first character.
The structure of the Contains method for the TrieWithOneChild class is similar to the TrieWithManyChildren class. Specifically, the
empty string needs to be handled first (after checking that the string isn’t null) and in exactly the same way,
as the empty string is represented in the same way in all three
implementations. Nonempty strings, however, are represented
differently, and hence need to be handled differently. For TrieWithOneChild, we need to check to
see if the first character of the given string matches the child’s
label. If so, we can recursively look for the remainder of the
string in that child. Otherwise, we should simply return false,
as this string is not in this trie.
The Add method for TrieWithOneChild will need five cases:
- A null string: This case can be handled in the same way as for TrieWithManyChildren.
- The empty string: This case can be handled in the same way as
for TrieWithManyChildren.
- A nonempty string whose first character is not a lower-case letter: An exception should be thrown.
- A nonempty string whose first character matches the child’s
label: The remainder of the string can be added to the child
using the child’s Add method. Because this method may return a
different node, we need to replace the child with the value this
method returns. We can then return this, as we didn’t need more
room for the given string.
- A nonempty string whose first character is a lower-case letter but does not match the
child’s label. In this case, we need to return a new
TrieWithManyChildren containing the given string and all of
the information already being stored.
The TrieWithNoChildren class is the simplest of the three, as we don’t need to worry about any children. The only private field it needs is a bool to indicate whether it stores the empty string. Its Contains method needs to handle null or empty strings in the same way as for the other two classes, but because a TrieWithNoChildren cannot contain a nonempty string, this method can simply return false when it is given a nonempty string.
The Add method for TrieWithNoChildren will need to handle a null or
empty string in the same way as the the other two classes. However,
this implementation cannot store a nonempty string. In this case, it
will need to construct and return a new TrieWithOneChild containing
the string to be added and the bool stored in this node.
Code that uses such a trie will need to refer to it as an ITrie
whenever possible. The only exception to this rule occurs when we are
constructing a new trie, as we cannot construct an instance of an
interface. Here, we want to construct the simplest implementation — a
TrieWithNoChildren. Otherwise, the only difference in usage as
compared to the implementation of the previous
section
is that the
Add method now returns the resulting trie, whose root may be a
different object; hence, we will need to be sure to replace the current
trie with whatever the Add method returns.
Traversing a Trie
Traversing a Trie
As with other kinds of trees, there are occasions where we need to
process all the elements stored in a trie in order. Here, the elements
are strings, which are not stored explicitly in the trie, but implicitly
based on the labels of various nodes. Thus, an individual node does not
contain a string; however, if its bool has a value of true,
then the path to that node describes a string stored in the trie. We can
therefore associate this string with this node. Note that this string is
a prefix of any string associated with any node in any of this node’s
children; hence, it is alphabetically less than any string found in any
of the children. Thus, in order to process each of the strings in
alphabetic order, we need to do a preorder
traversal
, which
processes the root before recursively processing the children.
In order to process the string associated with a node, we need to be
able to retrieve this string. Because we will have followed the path
describing this string in order to get to the node associated with it,
we can build this string on the way to the node and pass it as a
parameter to the preorder traversal of the trie rooted at this node.
Because we will be building this string a character at a time, to do
this efficiently we should use a
StringBuilder
instead of a string. Thus, the preorder traversal method for a trie
will take a StringBuilder parameter describing the path to that
trie, in addition to any other parameters needed to process the strings
associated with its nodes.
Before we present the algorithm itself, we need to address one more
important issue. We want the StringBuilder parameter to describe the
path to the node we are currently working on. Because we will need to do
a recursive call on each child, we will need to modify the
StringBuilder to reflect the path to that child. In order to be able
to do this, we will need to ensure that the recursive calls don’t change
the contents of the StringBuilder (or more precisely, that they undo
any changes that they make).
Because we are implementing a preorder traversal, the first thing we
will need to do is to process the root. This involves determining
whether the root is associated with a string contained in the trie, and
if so, processing that string. Determining whether the root is
associated with a contained string is done by checking the bool at
the root. If it is true, we can convert the StringBuilder
parameter to a string and process it by doing whatever processing
needs to be done for each string in our specific application.
Once we have processed the root, we need to recursively process each of
the children in alphabetic order of their labels. How we accomplish this
depends on how we are implementing the trie - we will assume the
implementation of the previous
section
. Because
this implementation uses three different classes depending on how many
children a node has, we will need to write three different versions of
the preorder traversal, one for each class. Specifically, after processing the root:
- For a TrieWithNoChildren, there is nothing more to do.
- Because a TrieWithOneChild has exactly one child, we need a
single recursive call on this child. Before we make this call, we
will need to append the child’s label to the StringBuilder.
Following the recursive call, we will need to remove the character
that we added by reducing its
Length
property by 1.
- We handle a TrieWithManyChildren in a similar way as a
TrieWithOneChild, only we will need to iterate through the
array of children and process each non-null child with a
recursive call. Note that for each of these children, its label will
need to be appended to the StringBuilder prior to the recursive
call and removed immediately after. We can obtain the label of a
child by adding the first letter of the alphabet to its array index and
casting
the result to a
char.
Tries in Word Games
Tries in Word Games
One application of tries is for implementing word games such as
Boggle® or Scrabble®. This section discusses how a trie can be
used to reduce dramatically the amount of time spent searching for words
in such games. We will focus specifically on Boggle, but the same
principles apply to other word games as well.
A Boggle game consists of either 16 or 25 dice with letters on their
faces, along with a tray containing a 4 x 4 or 5 x 5 grid
for holding these dice. The face of each die contains a single letter,
except that one face of one die contains “Qu”. The tray has a large
cover such that the dice can be placed in the cover and the tray placed
upside-down on top of the cover. The whole thing can then be shaken,
then inverted so that each die ends up in a different grid cell, forming
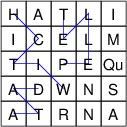
a random game board such as:


Players are then given a certain amount of time during which they
compete to try to form as many unique words as they can from these
letters. The letters of a word must be adjacent either horizontally,
vertically, or diagonally, and no die may be used more than once in a
single word. There is a minimum word length, and longer words are worth
more points. For example, the above game board contains the words,
“WITCH”, “ITCH”, “PELLET”, “TELL”, and “DATA”, among many others.

Suppose we want to build a program that plays Boggle against a human
opponent. The program would need to look for words on a given board. The
dictionary of valid words can of course be stored in a trie. In what follows,
we will show how the structure of a trie can be particularly helpful in
guiding this search so that words are found more quickly.
We can think of a search from a given starting point as a traversal of a
tree. The root of the tree is the starting point, and its children are
searches starting from adjacent dice. We must be careful, however, to
include in such a tree only those adjacent dice that do not already
occur on the path to the given die. For example, if we start a search at
the upper-left corner of the above board, its children would be the
three adjacent dice containing “I”, “C”, and “A”. The children of “I”,
then, would not include “H” because it is already on the path to “I”.
Part of this tree would look like this:
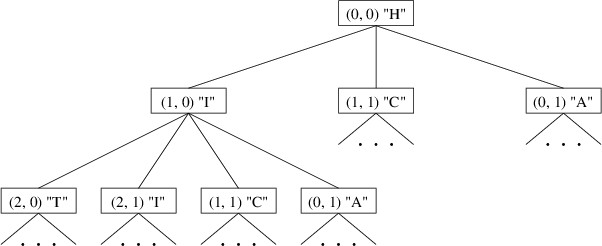

Note that this tree is not a data structure - it need not be explicitly
stored anywhere. Rather, it is a mathematical object that helps us to
design an algorithm for finding all of the words. Each word on the board
is simply a path in this tree starting from the root. We can therefore
traverse this tree in much the same way as we outlined in the previous
section
for tries.
For each node in the tree, we can look up the path leading to that node,
and output it if it is a word in the dictionary.
In order to be able to implement such a traversal, we need to be able to
find the children of a node. These children are the adjacent cells that
are not used in the path to the node. An efficient way to keep track of
the cells used in this path is with a bool[ , ] of the same
size as the Boggle board - a value of true in this array will
indicate that the corresponding cell on the board has been used in the
current path. The children of a node are then the adjacent cells whose
entries in this array are false.
A preorder traversal of this tree will therefore need the following
parameters (and possibly others, depending on how we want to output the
words found):
- The row index of the current cell.
- The column index of the current cell.
- The bool[ , ] described above. The current cell will
have a false entry in this array.
- A StringBuilder giving the letters on the path up to, but not
including, the current cell.
The preorder traversal will first need to update the cells used by
setting the location corresponding to the current cell to true.
Likewise, it will need to update the StringBuilder by appending the
contents of the current cell. Then it will need to process the root by
looking up the contents of the StringBuilder - if this forms a word,
it should output this word. Then it should process the children: for
each adjacent cell whose entry in the bool[ , ] is
false, it should make a recursive call on that cell. After all the
children have been processed, it will need to return the
bool[ , ] and the StringBuilder to their
earlier states by setting the array entry back to false and removing
the character(s) appended earlier.
Once such a method is written, we can call it once for each cell on the
board. For each of these calls, all entries in the bool[ , ]
should be false, and the StringBuilder should be empty.
While the algorithm described above will find all the words on a Boggle
board, a 5 x 5 board will require quite a while for the algorithm
to process. While this might be acceptable if we are implementing a game
that humans can compete with, from an algorithmic standpoint, we would
like to improve the performance. (In fact, there are probably better
ways to make a program with which humans can compete, as this search
will only find words that begin near the top of the board.)
We can begin to see how to improve the performance if we observe the
similarity between the trees we have been discussing and a trie
containing the word list. Consider, for example, a portion of the child
labeled ‘h’ in a trie representing a large set of words:
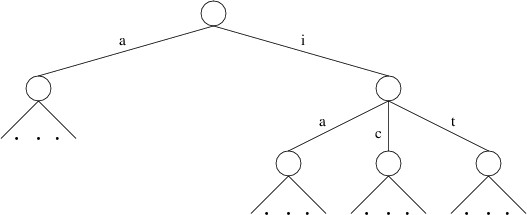

We have omitted some of the children because they are irrelevant to the
search we are performing (e.g., there is no die containing “E” adjacent
to “H” on the above game board). Also, we are assuming a minimum word
length of 4; hence, “ha”, “hi”, and “hit” are not shown as words in this
trie.
Notice the similarity between the trie portion shown above and the tree
shown earlier. The root of the tree has children representing dice
containing “I” and “A”, and the former node has children representing
dice containing “T”, “C”, and “A”; likewise, though they are listed in a
different order, the trie has children labeled ‘i’ and ‘a’, and the
former node has children labeled ’t’, ‘c’, and ‘a’.
What is more important to our discussion, however, is that the trie does
not have a child labeled ‘c’, as there is no English word beginning with
“hc”. Similarly, the child labeled ‘i’ does not have a child labeled
‘i’, as there is no English word beginning with “hii”. If there are no
words in the word list beginning with these prefixes, there is no need
to search the subtrees rooted at the corresponding nodes when doing the
preorder traversal. Using the trie to prune the search in this way ends
up avoiding many subtrees that don’t lead to any words. As a result,
only a small fraction of the original tree is searched.
In order to take advantage of the trie in this way, we need a method in
the trie implementation to return the child having a given label, or
null if there is no such child. Alternatively, we might provide a
method that takes a string and returns the trie that this string
leads to, or null if there is no such trie (this method would make
it easier to handle the die containing “Qu”). Either way, we can then
traverse the trie as we are doing the preorder traversal described
above, and avoid searching a subtree whenever the trie becomes null.
This revised preorder traversal needs an extra parameter - a trie giving
all completions of words beginning with the prefix given by the
StringBuilder parameter. We will need to ensure that this parameter
is never null. The algorithm then proceeds as follows:
- From the given trie, get the subtrie containing the completions of
words beginning with the contents of the current cell.
- If this subtrie is not null:
- Set the location in the bool[ , ] corresponding to
the current cell to true.
- Append the contents of the current cell to the
StringBuilder.
- If the subtrie obtained above contains the empty string,
output the contents of the StringBuilder as a word found.
- Recursively traverse each adjacent cell whose corresponding
entry in the bool[ , ] is false. The recursive
calls should use the subtrie obtained above.
- Set the location in the bool[ , ] corresponding to
the current cell to false.
- Remove the contents of the current cell from the end of the
StringBuilder (i.e., decrease its Length by the
appropriate amount).
We would then apply the above algorithm to each cell on the board. For
each cell, we would use a bool[ , ] whose entries are all
false, an empty StringBuilder, and the entire trie of valid words. Note that we
have designed the preorder traversal so that it leaves each of these
parameters unchanged; hence, we only need to initialize them once. The
resulting search will find all of the words on the board quickly.






