The Dictionary<TKey, TValue> Class

In this section, we will discuss the use of the Dictionary<TKey, TValue> class, which implements a dictionary. In the next section , we will discuss how this data structure can be implemented using a linked list. In subsequent sections, we will consider alternative implementations.

Note that the Dictionary<TKey, TValue> type has two type parameters, TKey and TValue. TKey is the type of the keys, and TValue is the type of the values (i.e., the data elements associated with the keys). Keys must always be non-null — any attempt to use a null key will result in an ArgumentNullException. A Dictionary<TKey, TValue>’s most basic public methods are:

• void Add(TKey key, TValue value) : Associates the given value with the given key. If there is already a value associated with the given key, it throws an ArgumentException.
• bool Remove(TKey key) : Removes the given key and its associated value from the dictionary, and returns whether the key was found.
• bool TryGetValue(TKey key, out TValue? value) : Returns whether the given key is in the dictionary. If so, the out parameter value is assigned the value associated with key; otherwise, value is assigned the default value for its type.

The above methods can be used for building and updating a Dictionary, as well as for looking up values by their keys. It is also possible to do updates and lookups using indexing. Specifically, a key may be used as an index in a Dictionary, as if the Dictionary were an array. For example, suppose that dictionary is a Dictionary<TKey, TValue>, k is a TKey, and v is a TValue. We can then do the following:

dictionary[k] = v;

This will associate the value v with the key k, as the Add method does; however, its behavior is slightly different if k already has a value associated with it. Whereas the Add method would throw an exception in this case, using the indexer will simply replace the value previously associated with k by the new value v. Thus, we use the Add method when we expect the key to be a new key for the dictionary, but we use the indexer when we want to associate the value with the key, regardless of whether the key is already in the dictionary.

Likewise, we can use the indexer to look up a key:

v = dictionary[k];

Again, the behavior is similar to the TryGetValue method, but slightly different, as there is no bool in the above statement. When using the indexer, if the key is not in the dictionary, it will throw a KeyNotFoundException. Thus, we use the indexer when we expect the key to be in the dictionary, but we use the TryGetValue method when we don’t know if the key is in the dictionary.

Implementing a Dictionary with a Linked List

One way of implementing a dictionary is to store all the keys and values in a linked list. We want to do this in such a way that a key is stored together with its associated value. To facilitate this, .NET provides a structure KeyValuePair<TKey, TValue> in the System.Collections.Generic namespace. This structure is used simply for storing a key and a value. The type parameter TKey is used to define the type of the keys, and the other type parameter TValue is used to define the type of the values. It has two public properties:

• Key , which gets the key stored; and
• Value , which gets the value stored.

Note that neither of these properties can be set; i.e., the structure is immutable. In order to set the key and value, we need to construct a new instance using its 2-parameter constructor . The first parameter to this constructor is the key, and the second is the value.

Now that we have a way of storing keys and values together, we can implement a Dictionary<TKey, TValue> with a linked list comprised of instances of LinkedListCell<KeyValuePair<TKey, TValue>>. Thus, each cell of the list stores as its Data a KeyValuePair<TKey, TValue> containing a key and its associated value. To add a key and a value, we first need to search the list for a cell containing that key. If we find such a cell, we either replace the KeyValuePair in that cell with a new KeyValuePair containing the given key and value, or we throw an exception, depending on the specific behavior required. If we don’t find such a cell, we insert a new cell containing the given key and value. Because it doesn’t matter where we insert it, we might as well insert it at the beginning of the list, as that is the easiest way. We can remove a key using techniques described in “Finding Prime Numbers” .

The main disadvantage to this approach is that searching for a key is expensive. For example, to search for a key that is not in the dictionary, we need to examine every key in the dictionary. We would like to improve on this performance.

One way of improving the performance of searching is to store the keys in increasing order. Then as we search, if we see a key that is larger than the key we are looking for, we can stop. However, recall that keys can be of any type. For some types of keys, “increasing order” and “larger than” make no sense.

C# does provide a way to restrict the types that can be passed as type parameters to generic types. Specifically, we can restrict the type TKey by writing the class statement as follows:

public class Dictionary<TKey, TValue> where TKey : notnull, IComparable<TKey>   

The where clause in this statement constrains TKey in two ways:

• notnull constrains it to be a non-nullable type. The compiler doesn’t actually enforce this constraint, but will give a warning if a nullable type is used for TKey.

• IComparable<TKey> constrains it to be a subtype of IComparable<TKey> . Each subtype of IComparable<TKey> contains a method public int CompareTo(TKey? x) . If a and b are of type TKey, then a.CompareTo(b) returns:

  • A negative number if a is considered to be less than b;
  • 0 if a is considered to be equal to b; or
  • A positive number if a is considered to be greater than b or if b is null.

We can therefore use this CompareTo method to keep the list in increasing order.

Note that by constraining the key type in this way, we are making the Dictionary<TKey, TValue> less general, as we may sometimes want to use a key type that can’t be ordered. On the other hand, there are times when not only do we have a key type that can be ordered, but also we need to access the keys in increasing order (for example, to print an ordered list of keys with their values). In such cases, what we actually need is an ordered dictionary, which both restricts the keys in this way and provides a means of accessing them in increasing order. While we won’t consider the full implementation of an ordered dictionary here, it is worth considering how we can improve performance by keeping the keys in increasing order.

Let’s now consider how to add a key and value to a linked list storing keys in increasing order. We first need to find where the key belongs in the ordering. Specifically, the cell whose Next property needs to be changed (assuming the key is not already in the list) is the one that must precede the new cell. We therefore need to find the last cell whose key is less than the key we need to add. Note also that when we are removing a key, the cell whose Next property needs to be changed is the last cell whose key is less than the key we are removing. Furthermore, if we are looking up a key, we need to look in the cell that follows the last cell whose key is less than the key we are looking for. This suggests that we should provide a private method to find the last cell whose key is less than a given key, provided such a cell exists.

Before we can write such a method, however, we first need to address a problem that occurs if we are trying to add, remove, or look up a key that is smaller than all other keys in the list. In this case, there are no cells containing keys smaller than the given key.

We can avoid needing a special case to deal with this problem if we include a special header cell at the beginning of our linked list. This cell will not contain any meaningful data, but it will always be present. If we consider that its key is less than any other key (though we will never actually examine its key), then there will always be at least one key less than any given key. We can obtain this header cell by initializing the linked list to contain a new cell containing the default key-value pair, rather than to null. Note that because the linked list will always contain at least the header cell, the reference to it should not be nullable.

A method to find the last cell containing a key less than a given key is now straightforward. We initialize a variable to the first cell (i.e., the header cell), and set up a loop that iterates as long as the next cell is non-null and contains a key less than the given key. Each iteration advances to the next cell. When the loop terminates, we return the cell we have reached.

To look up a key, we use the above method to find the last cell containing a key less than the key we are looking for. If the next cell is non-null and contains the key we are looking for, then we have found it; otherwise, it cannot be in the list. To add a key and value, we first need to look up the key in the same way. If we don’t find it, we insert a new cell containing this key and value following the last cell containing a key less than this key. To remove a key, we proceed in a similar way, but if we find the key, we remove this cell from the list.

While keeping the keys in increasing order improves the performance of many searches, the overall performance is still unsatisfactory for even data sets of moderate size. In subsequent sections, we will explore ways of improving this performance using various data structures.

Implementing a Dictionary with an Array-Like Structure

In the previous section , we discussed how linked lists could be used to implement a dictionary. An alternative to a linked list would be an array. A couple of other alternatives are the non-generic System.Collections.ArrayList or the generic System.Collections.Generic.List<T> . These classes are similar to singly-dimensioned arrays, but they can grow as needed. In this respect, they are like a StringBuilder , but instead of storing chars, an ArrayList stores object?s and a List<T> stores instances of the type parameter T. Elements can be retrieved from instances of these classes using indexing, just like retrieving an element from an array.

Assuming we restrict the keys to be non-nullable sub-types of IComparable<TKey>, where TKey is the key type, we can store the keys in order in any of these data structures. We can then search for a key in the same way as we described for a linked list. However, such a search can be expensive - to search for a key that is larger than any key in the dictionary, we need to examine all of the keys. We say that the performance of this sequential search is in $ O(n) $, where $ n $ is the number of keys in the dictionary. This means that as $ n $ grows, the time required for the search is at worst proportional to $ n $.

We can improve this performance dramatically for an array or array-like structure such as an ArrayList or a List<T> using a technique called binary search (there isn’t much we can do to improve the performance of searching a linked list, as its structure restricts us to traversing it sequentially). The idea is similar to what humans do when looking for something in an ordered list such as a dictionary or an index of a book. Rather than looking sequentially through the sequence, we first look in the middle and narrow our search space depending on how what we are looking for compares with what we are looking at. For example, if we are looking for “Les Miserables”, we first look in the middle of the sequence, where we might see “Othello”. Because “Les Miserables” is alphabetically less than “Othello”, we can narrow the search space to those titles less than “Othello”. In the middle of this search space, we might find the title, “Great Expectations”. Because “Les Miserables” is alphabetically greater than “Great Expectations”, we narrow the search space to those titles greater than “Great Expectations” and less than “Othello”. We continue narrowing in this way until either we find “Les Miserables” or the search space becomes empty, implying that the data set does not contain this title.

In a binary search, each lookup is as nearly as possible in the center of the search space. This means that each time we look at an entry, we either find what we are looking for, or we decrease the size of the search space to at most half its previous size. For large data sets the search space therefore shrinks rapidly. For example, if we start with 1,000,000 elements and repeatedly reduce the search space to at most half its previous size, after 20 such reductions, we are left with nothing. Likewise, if we start with 1,000,000,000 elements, 30 such reductions in size lead to an empty search space.

To implement this algorithm, we need to keep track of the search space. We will use two int variables, start and end. start will keep track of the first index in the search space, while end will keep track of the first index past the search space, as follows:

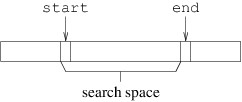
The way we have defined end may seem unnatural at first, but because it simplifies various calculations, it is a common way of describing a search space. For example, the number of elements in such a search space is simply the difference between end and start, and to describe an entire array, we can initialize start to 0 and end to the array’s length.

We then need a loop to iterate as long as this search space is nonempty (we can return from inside this loop if we find what we are looking for). On each iteration, we need to find the midpoint of the search space. This midpoint is simply the average of start and end - i.e., their sum divided by 2. We need to be a bit careful here because we are doing integer division, which may involve truncation. As a result, we may not get exactly the average. In any case, we need to ensure that the index we compute is within the search space - otherwise, we may not reduce the search space, and an infinite loop will result. Because the search space is nonempty, start < end; hence, the true average is strictly between start and end. If this average is not an integer, the result will be rounded down to the next smaller integer. Because start is an integer, this result will be no less than start, but less than end; hence it will be in the search space.

Once we have computed this midpoint, we need to compare the key of the element at that location with the key we are looking for. Recall that we use the CompareTo method to do this comparison. Note that for large key types, the CompareTo method can be expensive. For this reason, it is best to call the CompareTo method only once for a given pair of keys, and if necessary, save the result it returns in order to make more than one comparison between this result and 0.

Thus, once we have obtained the result of the CompareTo method, we need to determine which of the three cases we have. If the keys are equal, we should be able to return. If the key we are looking for is less than the key at the midpoint, we need to adjust end. Otherwise, we need to adjust start. We are then ready for the next iteration of the loop.

If the loop finishes without returning, then the search space is empty; hence, the key we are looking for is not in the data set. However, start will end up at the point at which this key could be inserted; hence, the binary search can be used for both lookups and insertions.

Binary search is a very efficient way to search an ordered array-like structure. In particular, it always makes no more than $ O(\log n) $ comparisons, where $ n $ is the number of elements in the data set. The $ \log $ function grows very slowly - much more slowly than $ n $.